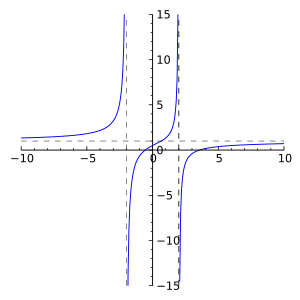
 This year, after the SAT on Oct 6th, I started my precalculus lesson. One of the sections that we covered in this term is called the Rational Function. If you didn’t know or forget what it is, it’s a function in the form of r(x) = P(x)/Q(x), where P and Q are both polynomials and have graph that look like the picture at your left. It was quite difficult for me at first to graph this function but once I noticed the pattern, it was fairly easy and straightforward.
This year, after the SAT on Oct 6th, I started my precalculus lesson. One of the sections that we covered in this term is called the Rational Function. If you didn’t know or forget what it is, it’s a function in the form of r(x) = P(x)/Q(x), where P and Q are both polynomials and have graph that look like the picture at your left. It was quite difficult for me at first to graph this function but once I noticed the pattern, it was fairly easy and straightforward.
In order to graph this rational function:
- Factor the numerator and denominator
- Look for intercepts: x-intercept is equal to the zeros of the numerator and y-intercept is equal to C value of numerator divide denominator
- Find the vertical asymptotes by determine the zeros of the denominator
- Figure out the horizontal asymptote by using the rule below.
- Sketch the graph
r(x)= (x-2)/(x^2-2x-8) ==> (x-2)/(x-4)(x+2) x-intercept: 2 y-intercept: 1/4 vertical asymptote: -2, 4 horizontal asymptote: 0 slant asymptote: none
We also learned about slant asymptote, where the degree of the numerator is one greater than the denominator. This also means that there will be no horizontal asymptote. We determined the slant asymptote by divide polynomials with each other and we did not obtain its remainder. Example below!
r(x)= (x^3+8)/(x^2-x-2) ==> (x^3+8)/(x-2)(x+1) x-intercept: -2 y-intercept: -4 vertical asymptote: -1,2 horizontal asymptote: none slant asymptote: y = x+1




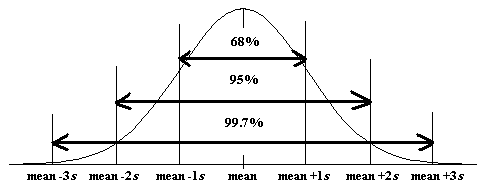
 AP Statistic contents encompass of many critical lessons and the normal distribution is one of them. Normal Distribution use to describe data that is symmetric (with a single peak) and follow the empirical rules (68-95-99.7). The empirical rules provide an estimate of the data spread using the mean and standard deviation. When the data follows the empirical rules, about 68% of the data is one standard deviation from the mean, 95% is two standard deviation from the mean, and 99.7% is three standard deviation from the mean. We can easily determine the data, whether it follows the empirical rules or not, through the normal curve. The area of the normal curves is always equal to 1.
AP Statistic contents encompass of many critical lessons and the normal distribution is one of them. Normal Distribution use to describe data that is symmetric (with a single peak) and follow the empirical rules (68-95-99.7). The empirical rules provide an estimate of the data spread using the mean and standard deviation. When the data follows the empirical rules, about 68% of the data is one standard deviation from the mean, 95% is two standard deviation from the mean, and 99.7% is three standard deviation from the mean. We can easily determine the data, whether it follows the empirical rules or not, through the normal curve. The area of the normal curves is always equal to 1.